1.4.5.1.1. 数据结构
1.4.5.1.1.1. 线性结构
线性结构作为最常用的数据结构,其特点是数据元素之间一对一的线性关系
线性结构有两种不同的存储结构,即顺序存储结构和链式存储结构.顺序存储线性表称为顺序表,顺序表的存储元素是连续的
链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息。
线性结构常见的是:数组、队列、链表和栈
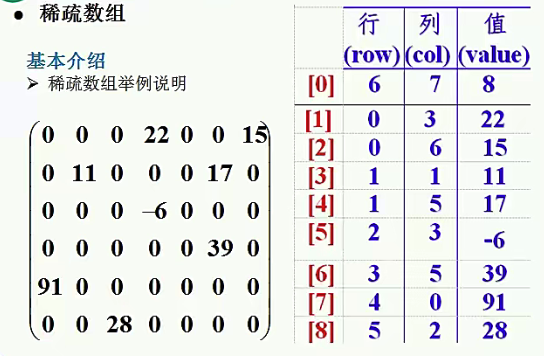
稀疏数组(sparsearray)
当一个数组中的元素大部分元素都为0,或者同一个值的数据组时,可以用稀疏数组来保存
1、记录数组一共几行几列,有多少不同的值
2、把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
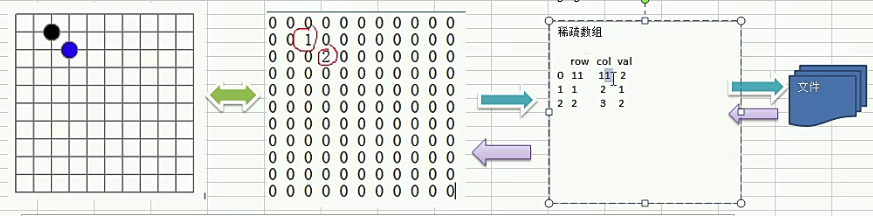
二维数组转稀疏数组的思路
遍历 原始的二维数组,得到有效数据的个数sum 2.根据sum就可以创建稀疏数组sparseArr intisum+ 1) 131
将二维数组的有效数据数据存入到稀疏数组
稀疏数组转原始的二维数组的思路
先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的chessArr2=int/1111
- 在读取稀疏数组后几行的数据,并赋给
/**
* 稀疏数组
* - 二维数组转稀疏数组的思路
*
* 1. 遍历 原始的二维数组,得到有效数据的个数sum
* 2. 根据sum就可以创建稀疏数组sparseArr intisum+ 1)
* 3. 将二维数组的有效数据数据存入到稀疏数组
*
* - 稀疏数组转原始的二维数组的思路
*
* 1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的chessArr2=int/1111
* 2. 在读取稀疏数组后几行的数据,并赋给 原始的二维数组即可。
*/
public class SparseArray {
public static void main(String[] args) {
// 创建一个原始二维数组 11 * 11
// 0: 标识没有棋子 1 表示黑子 2 表示篮子
int chessArr1[][] = new int[11][11];
chessArr1[1][2] = 1;
chessArr1[2][3] = 2;
chessArr1[4][5] = 2;
// 输出原始二维数组
System.out.println("输出原始二维数组~~");
for (int[] row : chessArr1) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
// 将二维数组转稀疏数组
// 1. 先遍历二维数组,得到非0数据的个数
int sum = 0;
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
sum++;
}
}
}
// 2. 创建对应的稀疏数组
int sparseArr[][] = new int[sum + 1][sum];
// 给稀疏数组赋值
sparseArr[0][0] = 11;
sparseArr[0][1] = 11;
sparseArr[0][2] = sum;
// 遍历二维数组,将非0的值存放到稀疏数组中
int count = 0; //count 记录第几个非0 数据
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
count++;
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = chessArr1[i][j];
}
}
}
// 输出稀疏数组
System.out.println();
System.out.println("输出稀疏数组~~~~");
for (int i = 0; i < sparseArr.length; i++) {
System.out.printf("%d\t%d\t%d\t\n", sparseArr[i][0], sparseArr[i][1], sparseArr[i][2]);
}
System.out.println();
//将稀疏数组恢复
//1.先读取稀疏数组第一行,根据第一行的数据,创建原始二维数组
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
// 稀疏数组赋值原始数组,从第二行开始
for (int i = 1; i < sparseArr.length; i++) {
chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
// 恢复二维数组
System.out.println();
System.out.println("恢复二维数组");
for (int[] row : chessArr2) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
}
}
队列
队列是一个优先列表,可以用数组和链表实现
遵循先入先出的原则, 即:先存入队列的数据要先取出。后存入的要后取出
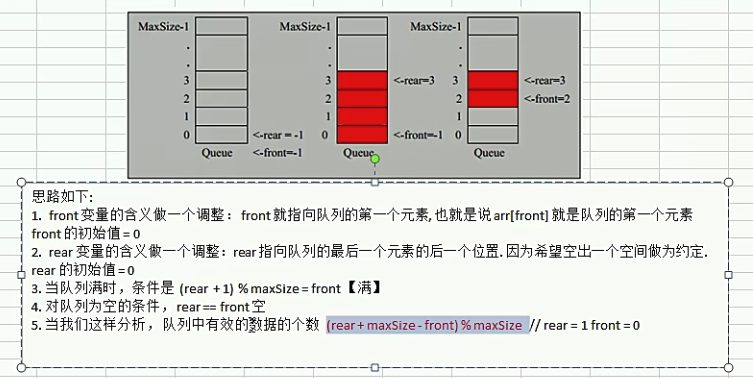
环形队列(CircleQueue)
链表(linked list )
有序的列表
链表是已节点的方式存储
每个节点包含data域、next域、指向下一个节点
单向链表查找方向只能是一个方向,而双向链表可以向前或者向后查找
单向链表不能自我删除,需要辅助节点,而双向链表可以自我删除
栈
先入后出
应用场景:
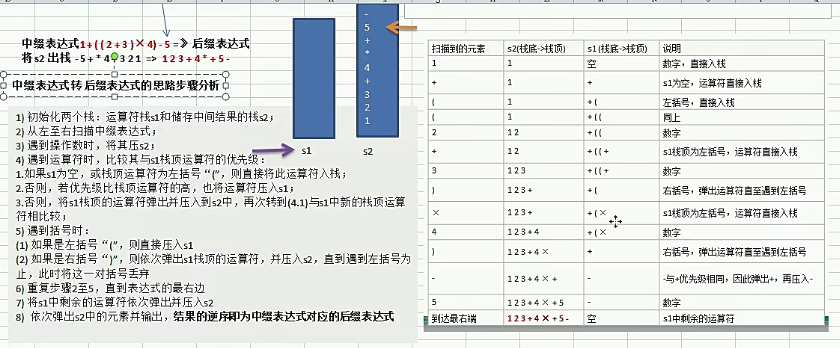
表达式转换:前缀(波兰表达式)、中缀表达式转后缀(逆波兰)表达式与求值
前缀表达式运算符位于操作数之前:从右至左扫描
后缀表达式与前缀相似,只是运算符位于操作数之后
二叉树遍历
图形深度优先

递归
方法的局部变量是独立,不会相互影响(引用对象除外)
递归必须有退出条件
一个方法执行完毕,或者遇到return,就会返回,遵循谁调用就将结果返回给谁。
1.4.5.1.1.2. 非线性结构
二维数组、多维数组、广义表、树结构、图结构
二叉树
能提高存储、读取效率;每个节点最多只能有两个子节点的形式
前序遍历:先输出父节点,在遍历左子树和右子树
中序遍历: 先遍历左子树,在输出父节点,在遍历右子树
后续遍历:先遍历左子树,在遍历右子树,最后输出父节点
看父节点输出顺序:先输出父节点就是前序、中间输出父节点就是中序、后输出父节点就是后序
顺序存储二叉树
只考虑完全二叉树
第n个左子节点2*n+1
第n个右子节点2*n+2
第n个元素父节点 (n-1)/2
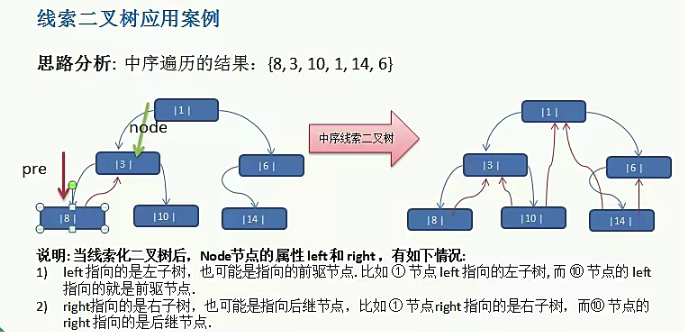
线索化二叉树(threaded binaryTree)
n个节点的二叉链表中含有n+1(2n-(n-1) = n +1)个空值针域。
赫夫曼树/(哈夫曼树)
给定n个权值作为n个叶子节点,构造一颗二叉树。若该数带权路径长度wpl达到最小,被称为二叉树最优二叉树.也称为哈夫曼树(HuffMan tree)
Wpl 最小二叉树就是赫夫曼树
树的带权路径长度:所有叶子节点的带权路径长度之和(wpl),权值越大的节点离根节点越近二叉树才是最优二叉树
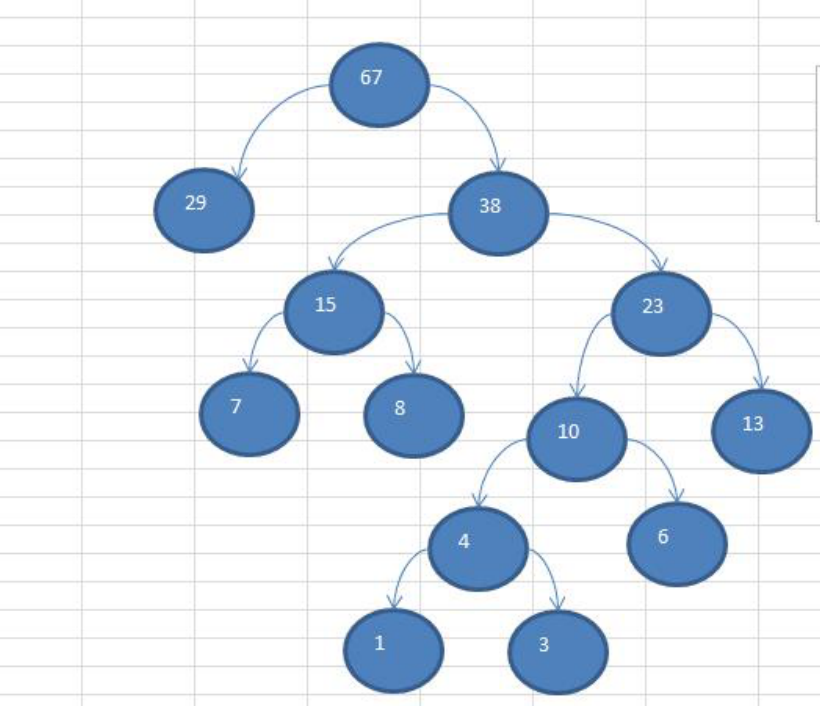
构建树的步骤:{13,7,8,3,29,6,1}
1、从小达到排序,将每个数据看成最简单的二叉树.
2、取出根节点权值最小的两颗二叉树
3、组成一颗新的二叉树,改新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
4、在将新的二叉树已根权值大小排序,不断重复1、2、3、4 直到所有数据都被处理
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = {13, 7, 8, 3, 29, 6, 1};
Node root = createHuffmanTree(arr);
//测试一把
preOrder(root); //
}
//编写一个前序遍历的方法
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("是空树,不能遍历~~");
}
}
// 创建赫夫曼树的方法
/**
*
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好后的赫夫曼树的root结点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1. 遍历 arr 数组
// 2. 将arr的每个元素构成成一个Node
// 3. 将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
//我们处理的过程是一个循环的过程
while (nodes.size() > 1) {
//排序 从小到大
Collections.sort(nodes);
System.out.println("nodes =" + nodes);
//取出根节点权值最小的两颗二叉树
//(1) 取出权值最小的结点(二叉树)
Node leftNode = nodes.get(0);
//(2) 取出权值第二小的结点(二叉树)
Node rightNode = nodes.get(1);
//(3)构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//(4)从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
//(5)将parent加入到nodes
nodes.add(parent);
}
//返回哈夫曼树的root结点
return nodes.get(0);
}
}
// 创建结点类
// 为了让Node 对象持续排序Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node> {
int value; // 结点权值
char c; //字符
Node left; // 指向左子结点
Node right; // 指向右子结点
//写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
// 表示从小到大排序
return this.value - o.value;
}
}
赫夫曼编码(算法) / 哈夫曼编码
无损压缩
广泛用于数据文件压缩,压缩率通常在20%~90%, 是可变长编码(VLC)的一种
变长编码:按照每个字符出现次数进行编码,原则出现次数越多编码越小
原理:
1、统计字符出现个数,排序个数后创建哈夫曼树
2、根据哈夫曼树给各个字符编码, 在左路径为0 向右为1
平衡二叉树(avl)
一颗空树或它的左右两个子树高度差绝对值不超过1,并且左右两个子树都是一颗平衡二叉树,
常见实现方法:红黑树、avl算法 、替罪羊树、treap、伸展树等
多路查找树
图
二维数组表示(邻接矩阵);链表(邻接表,使用数组+链表组成)
深度优先:每次都在访问完当前节点后首先访问当前节点的第一个邻接节点;优先往纵向挖掘深入,而不是对一个节点所有邻接节点进行横向访问
1.4.5.1.1.3. 哈希表
通过关键码映射到表中位置来访问记录,以加快查找速度。
1.4.5.1.2. 算法
时间复杂度:
事后统计法:同一台计算机相同状态下运行,才能比较哪个算法那速速快
事前估算法:通过分析某个算法的时间复杂度判断算法更优
时间频度:一个算法语句执行次数称为语句频度或时间频度。T(n), 行号:52
忽略常数项、忽略低次项、忽略系数
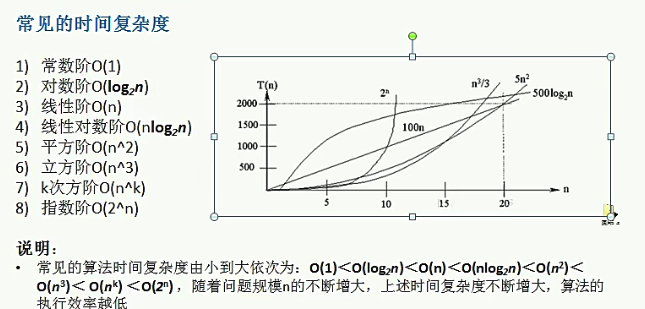
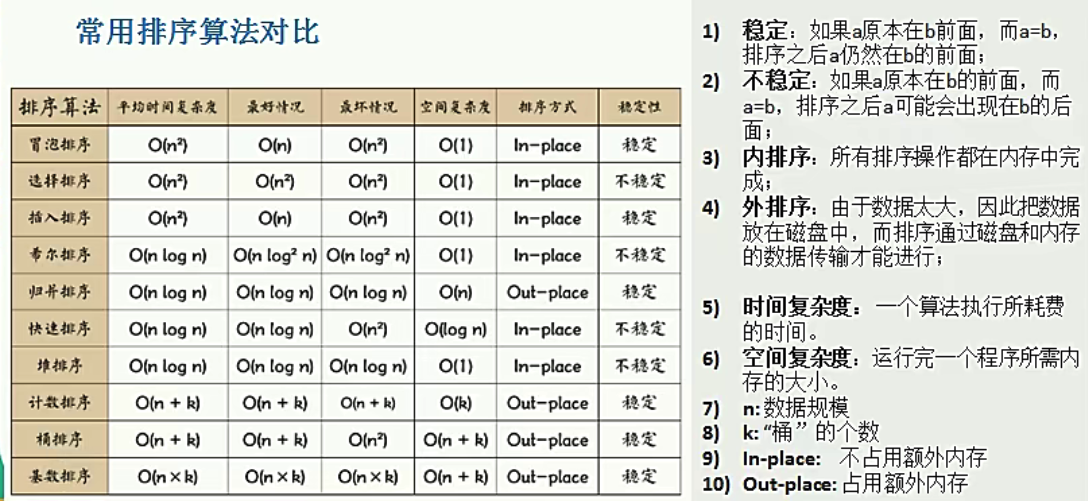
1.4.5.1.2.1. 排序算法
按类别分为:内部排序、外部排序
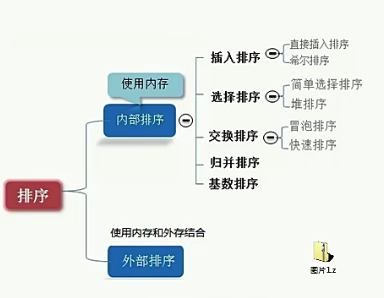
冒泡排序
依次比较相邻元素值,发现逆序则交换,使值较大的元素逐渐从前向后移动
// 将前面额冒泡排序算法,封装成一个方法
public static void bubbleSort(int[] arr) {
// 冒泡排序 的时间复杂度 O(n^2), 自己写出
int temp = 0; // 临时变量
boolean flag = false; // 标识变量,表示是否进行过交换
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1]) {
flag = true;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
//System.out.println("第" + (i + 1) + "趟排序后的数组");
//System.out.println(Arrays.toString(arr));
if (!flag) { // 在一趟排序中,一次交换都没有发生过
break;
} else {
flag = false; // 重置flag!!!, 进行下次判断
}
}
}
选择排序
按指定规则选出某一元素,在依规定交换位置达到排序目录。选择排序比冒泡排序快
循环中找到最小值,每轮循环中进行最小值和当前索引值进行交换
public static void selectSort(int[] arr) {
//选择排序时间复杂度是 O(n^2)
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) { // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[i], 即交换
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
插入排序
将n个待排序的元素看成一个有序和一个无序表,开始时有序表只有1个元素,无序表包含n-1个元素,排序过程中将无序表中元素一次与有序元素排序码比较,将它插入到适当位置
1、定义待插入的值、待插入记录索引
2、拿后一个值与当前待插入值比较,比较不通过交换,并后移再次比较待插入值并判断是否交换
3、给待插入值赋需要的索引位置
public static void insertSort(int[] arr) {
int insertVal = 0;
int insertIndex = 0;
for(int i = 1; i < arr.length; i++) {
//定义待插入的数
insertVal = arr[i];
insertIndex = i - 1; // 即arr[i]的前面这个数的下标
// 给insertVal 找到插入的位置
// 说明
// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[insertIndex] 后移
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
insertIndex--;
}
// 当退出while循环时,说明插入的位置找到, insertIndex + 1
// 举例:理解不了,我们一会 debug
//这里我们判断是否需要赋值
if(insertIndex + 1 != i) {
arr[insertIndex + 1] = insertVal;
}
//System.out.println("第"+i+"轮插入");
//System.out.println(Arrays.toString(arr));
}
}
希尔排序(缩小增量排序)
把记录按下标一定增量分组,对每组直接插入排序算法排序.
希尔排序对有序列表插入时可以采用交换法和插入法、移位法
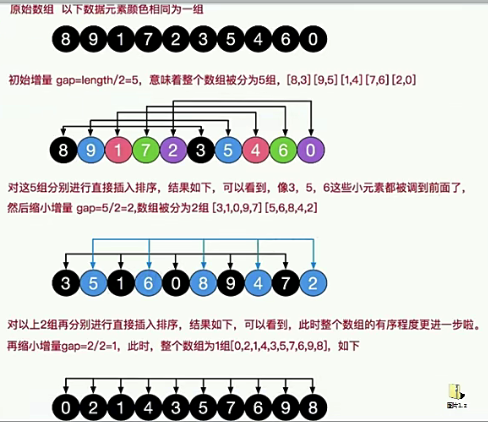
// 使用逐步推导的方式来编写希尔排序
// 希尔排序时, 对有序序列在插入时采用交换法,
// 思路(算法) ===> 代码
public static void shellSort(int[]arr){
int temp=0;
int count=0;
// 根据前面的逐步分析,使用循环处理
for(int gap=arr.length/2;gap>0;gap/=2){
for(int i=gap;i<arr.length;i++){
// 遍历各组中所有的元素(共gap组,每组有个元素), 步长gap
for(int j=i-gap;j>=0;j-=gap){
// 如果当前元素大于加上步长后的那个元素,说明交换
if(arr[j]>arr[j+gap]){
temp=arr[j];
arr[j]=arr[j+gap];
arr[j+gap]=temp;
}
}
}
//System.out.println("希尔排序第" + (++count) + "轮 =" + Arrays.toString(arr));
}
}
//对交换式的希尔排序进行优化->移位法
public static void shellSort2(int[]arr){
// 增量gap, 并逐步的缩小增量
for(int gap=arr.length/2;gap>0;gap/=2){
// 从第gap个元素,逐个对其所在的组进行直接插入排序
for(int i=gap;i<arr.length;i++){
int j=i;
int temp=arr[j];
if(arr[j]<arr[j-gap]){
while(j-gap>=0&&temp<arr[j-gap]){
//移动
arr[j]=arr[j-gap];
j-=gap;
}
//当退出while后,就给temp找到插入的位置
arr[j]=temp;
}
}
}
}
快速排序(递归)
通过遍历让排序的数据分割独立两部分,其中一部分数据比另一部分要小。
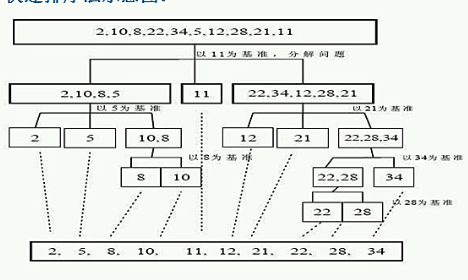
public static void quickSort(int[] arr,int left, int right) {
int l = left; //左下标
int r = right; //右下标
//pivot 中轴值
int pivot = arr[(left + right) / 2];
int temp = 0; //临时变量,作为交换时使用
//while循环的目的是让比pivot 值小放到左边
//比pivot 值大放到右边
while( l < r) {
//在pivot的左边一直找,找到大于等于pivot值,才退出
while( arr[l] < pivot) {
l += 1;
}
//在pivot的右边一直找,找到小于等于pivot值,才退出
while(arr[r] > pivot) {
r -= 1;
}
//如果l >= r说明pivot 的左右两的值,已经按照左边全部是
//小于等于pivot值,右边全部是大于等于pivot值
if( l >= r) {
break;
}
//交换
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//如果交换完后,发现这个arr[l] == pivot值 相等 r--, 前移
if(arr[l] == pivot) {
r -= 1;
}
//如果交换完后,发现这个arr[r] == pivot值 相等 l++, 后移
if(arr[r] == pivot) {
l += 1;
}
}
// 如果 l == r, 必须l++, r--, 否则为出现栈溢出
if (l == r) {
l += 1;
r -= 1;
}
//向左递归
if(left < r) {
quickSort(arr, left, r);
}
//向右递归
if(right > l) {
quickSort(arr, l, right);
}
}
归并排序(分治-递归)
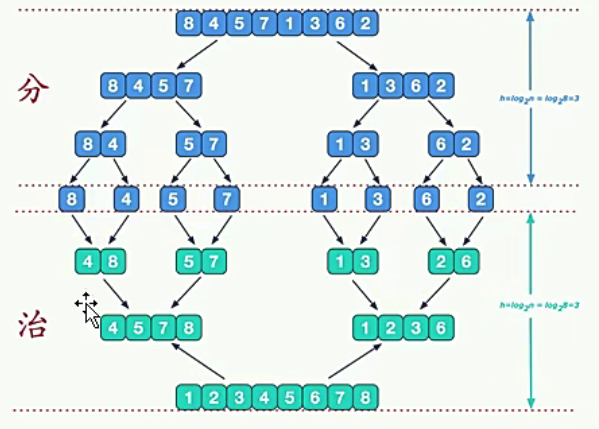
//分+合方法
public static void mergeSort(int[]arr,int left,int right,int[]temp){
if(left<right){
int mid=(left+right)/2; //中间索引
//向左递归进行分解
mergeSort(arr,left,mid,temp);
//向右递归进行分解
mergeSort(arr,mid+1,right,temp);
//合并
merge(arr,left,mid,right,temp);
}
}
//合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[]arr,int left,int mid,int right,int[]temp){
int i=left; // 初始化i, 左边有序序列的初始索引
int j=mid+1; //初始化j, 右边有序序列的初始索引
int t=0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while(i<=mid&&j<=right){//继续
//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
//即将左边的当前元素,填充到 temp数组
//然后 t++, i++
if(arr[i]<=arr[j]){
temp[t]=arr[i];
t+=1;
i+=1;
}else{ //反之,将右边有序序列的当前元素,填充到temp数组
temp[t]=arr[j];
t+=1;
j+=1;
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while(i<=mid){ //左边的有序序列还有剩余的元素,就全部填充到temp
temp[t]=arr[i];
t+=1;
i+=1;
}
while(j<=right){ //右边的有序序列还有剩余的元素,就全部填充到temp
temp[t]=arr[j];
t+=1;
j+=1;
}
//(三)
//将temp数组的元素拷贝到arr
//注意,并不是每次都拷贝所有
t=0;
int tempLeft=left; //
//第一次合并 tempLeft = 0 , right = 1 // tempLeft = 2 right = 3 // tL=0 ri=3
//最后一次 tempLeft = 0 right = 7
while(tempLeft<=right){
arr[tempLeft]=temp[t];
t+=1;
tempLeft+=1;
}
}
基数排序(分配式排序)
桶分配,空间换时间的经典算法
1、找到数组中最大数
2、找到数组最大长度,得到最大分配桶的基数(即多少位的长度)
3、按基数比例按桶个数分配到不同的桶内
4、合并桶数据
//基数排序方法
public static void radixSort(int[] arr) {
//1. 得到数组中最大的数的位数
int max = arr[0]; //假设第一数就是最大数
for(int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//得到最大数是几位数
int maxLength = (max + "").length();
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
//说明
//1. 二维数组包含10个一维数组
//2. 为了防止在放入数的时候,数据溢出,则每个一维数组(桶),大小定为arr.length
//3. 名明确,基数排序是使用空间换时间的经典算法
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
//可以这里理解
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
//这里我们使用循环将代码处理
for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
//(针对每个元素的对应位进行排序处理), 第一次是个位,第二次是十位,第三次是百位..
for(int j = 0; j < arr.length; j++) {
//取出每个元素的对应位的值
int digitOfElement = arr[j] / n % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)
int index = 0;
//遍历每一桶,并将桶中是数据,放入到原数组
for(int k = 0; k < bucketElementCounts.length; k++) {
//如果桶中,有数据,我们才放入到原数组
if(bucketElementCounts[k] != 0) {
//循环该桶即第k个桶(即第k个一维数组), 放入
for(int l = 0; l < bucketElementCounts[k]; l++) {
//取出元素放入到arr
arr[index++] = bucket[k][l];
}
}
//第i+1轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!
bucketElementCounts[k] = 0;
}
//System.out.println("第"+(i+1)+"轮,对个位的排序处理 arr =" + Arrays.toString(arr));
}
}
堆排序
堆具有以下性质:
完全二叉树: 一般升序采用大顶堆,降序采用小顶堆
每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆 arr[i] >= arr[2*i+1]&&arr[i]>=arr[2*i+2]
每个节点的值都小于或等于其左右孩子节点的值,称为小顶堆 arr[i] <= arr[2*i+1]&&arr[i]<=arr[2*i+2]
排序规则:
1、将待排序序列构造成一个大顶堆
2、此时,整个序列最大值就是堆顶的根节点
3、将其与末尾元素进行交换,此时末尾就为最大值
4、然后将剩余n-1元素重新构造成一个堆,这样会得到n个元素的次小值
//编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
//将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
for(int i = arr.length / 2 -1; i >=0; i--) {
adjustHeap(arr, i, arr.length);
}
/*
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
*/
for(int j = arr.length-1;j >0; j--) {
//交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
}
//将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
* 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
* 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param lenght 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int lenght) {
int temp = arr[i];//先取出当前元素的值,保存在临时变量
//开始调整
//1. k = i * 2 + 1 k 是 i结点的左子结点
for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if(arr[k] > temp) { //如果子结点大于父结点
arr[i] = arr[k]; //把较大的值赋给当前结点
i = k; //!!! i 指向 k,继续循环比较
} else {
break;//!
}
}
//当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;//将temp值放到调整后的位置
}
1.4.5.1.2.2. 查找算法
线性查找
遍历,逐一比对
二分查找
前提是:必须是一个有序数组
思路:递归、非递归
/* 有多个相同的数值时,如何将所有的数值都查找到
*
* 思路分析
* 1. 在找到mid 索引值,不要马上返回
* 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 4. 将Arraylist返回
*/
public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch2(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch2(arr, left, mid - 1, findVal);
} else {
// * 思路分析
// * 1. 在找到mid 索引值,不要马上返回
// * 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 4. 将Arraylist返回
List<Integer> resIndexlist = new ArrayList<Integer>();
//向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
int temp = mid - 1;
while(true) {
if (temp < 0 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp -= 1; //temp左移
}
resIndexlist.add(mid); //
//向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
temp = mid + 1;
while(true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp += 1; //temp右移
}
return resIndexlist;
}
}
非递归
/**
* 二分查找的非递归实现
* @param arr 待查找的数组, arr是升序排序
* @param target 需要查找的数
* @return 返回对应下标,-1表示没有找到
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while(left <= right) { //说明继续查找
int mid = (left + right) / 2;
if(arr[mid] == target) {
return mid;
} else if ( arr[mid] > target) {
right = mid - 1;//需要向左边查找
} else {
left = mid + 1; //需要向右边查找
}
}
return -1;
}
插值查找(中间点)
类似于二分查找,不同的是插值从适应mid开始。要求数组有序
使用场景:数据量大、关键字分布均匀情况下,速度快。不均匀时效率不如二分

int mid = left + (right-left) * (findVal - arr[left]) / arr[right] - arr[left]) ;
/**
*
* @param arr 数组
* @param left 左边索引
* @param right 右边索引
* @param findVal 查找值
* @return 如果找到,就返回对应的下标,如果没有找到,返回-1
*/
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
System.out.println("插值查找次数~~");
//注意:findVal < arr[0] 和 findVal > arr[arr.length - 1] 必须需要
//否则我们得到的 mid 可能越界
if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
return -1;
}
// 求出mid, 自适应
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) { // 说明应该向右边递归
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 说明向左递归查找
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
斐波那契(黄金分割法)查找算法
在某些情况需要对原数组进行扩容
mid = low + F[k-1] -1 ; // F代表斐波那契数列
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int[] arr = {1, 8, 10, 89, 1000, 1234};
System.out.println("index=" + fibSearch(arr, 189));// 0
}
//因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列,因此我们需要先获取到一个斐波那契数列
//非递归方法得到一个斐波那契数列
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//编写斐波那契查找算法
//使用非递归的方式编写算法
/**
*
* @param a 数组
* @param key 我们需要查找的关键码(值)
* @return 返回对应的下标,如果没有-1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //表示斐波那契分割数值的下标
int mid = 0; //存放mid值
int f[] = fib(); //获取到斐波那契数列
//获取到斐波那契分割数值的下标
while (high > f[k] - 1) {
k++;
}
//因为 f[k] 值 可能大于 a 的 长度,因此我们需要使用Arrays类,构造一个新的数组,并指向temp[]
//不足的部分会使用0填充
int[] temp = Arrays.copyOf(a, f[k]);
//实际上需求使用a数组最后的数填充 temp
//举例:
//temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
for (int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
// 使用while来循环处理,找到我们的数 key
while (low <= high) { // 只要这个条件满足,就可以找
mid = low + f[k - 1] - 1;
if (key < temp[mid]) { //我们应该继续向数组的前面查找(左边)
high = mid - 1;
//为甚是 k--
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
//即 在 f[k-1] 的前面继续查找 k--
//即下次循环 mid = f[k-1-1]-1
k--;
} else if (key > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
low = mid + 1;
//为什么是k -=2
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
//4. 即在f[k-2] 的前面进行查找 k -=2
//5. 即下次循环 mid = f[k - 1 - 2] - 1
k -= 2;
} else { //找到
//需要确定,返回的是哪个下标
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
分治算法divide-and-conquer(汉若塔)
小盘不能放大大盘上,在3根柱子之间一次只能移动一个盘子

public class Hanoitower {
public static void main(String[] args) {
hanoiTower(10, 'A', 'B', 'C');
}
//汉诺塔的移动的方法
//使用分治算法
public static void hanoiTower(int num, char a, char b, char c) {
//如果只有一个盘
if (num == 1) {
System.out.println("第1个盘从 " + a + "->" + c);
} else {
//如果我们有 n >= 2 情况,我们总是可以看做是两个盘 1.最下边的一个盘 2. 上面的所有盘
//1. 先把 最上面的所有盘 A->B, 移动过程会使用到 c
hanoiTower(num - 1, a, c, b);
//2. 把最下边的盘 A->C
System.out.println("第" + num + "个盘从 " + a + "->" + c);
//3. 把B塔的所有盘 从 B->C , 移动过程使用到 a塔
hanoiTower(num - 1, b, a, c);
}
}
}
动态规划算法(dynamic programming)背包
应用场景=背包问题(物品不能重复,容量值固定(4),要求达到目标装入总价值最大化)
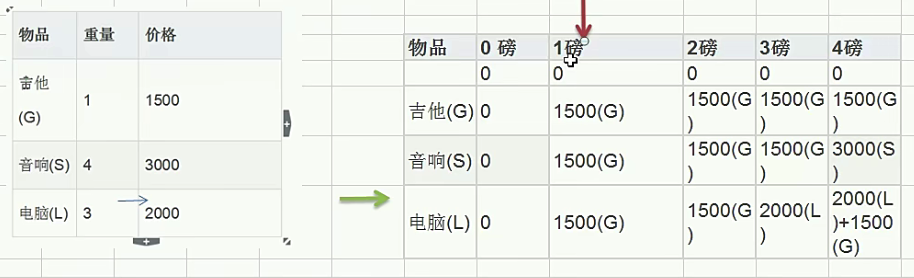
1、v[i][0]=v[0][j]=0 ;//表示填入表第一行和第一列为0
2、当w[i]>j时: v[i][j]=v[i-1][j] ;//当新增商品时,他的容量大于当前背包容量时,就直接使用上一个单元格值
3、当j>w[i]时:v[i][j]=max{v[i-1][j],v[i-1][j-w[i]+v[i]]}
//当准备新增商品容量小于等于当前背包容量,此时装入方式:
v[i-1][j] :就是上一个单元格装入的最大值
v[i]:表示当前商品价值
v[i-1][j-w[i]]: 装入i-1商品到剩余空间的最大值
public class KnapsackProblem {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] w = {1, 4, 3};//物品的重量
int[] val = {1500, 3000, 2000}; //物品的价值 这里val[i] 就是前面讲的v[i]
int m = 4; //背包的容量
int n = val.length; //物品的个数
//创建二维数组,
//v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
int[][] v = new int[n + 1][m + 1];
//为了记录放入商品的情况,我们定一个二维数组
int[][] path = new int[n + 1][m + 1];
//初始化第一行和第一列, 这里在本程序中,可以不去处理,因为默认就是0
for (int i = 0; i < v.length; i++) {
v[i][0] = 0; //将第一列设置为0
}
for (int i = 0; i < v[0].length; i++) {
v[0][i] = 0; //将第一行设置0
}
//根据前面得到公式来动态规划处理
for (int i = 1; i < v.length; i++) { //不处理第一行 i是从1开始的
for (int j = 1; j < v[0].length; j++) {//不处理第一列, j是从1开始的
//公式
if (w[i - 1] > j) { // 因为我们程序i 是从1开始的,因此原来公式中的 w[i] 修改成 w[i-1]
v[i][j] = v[i - 1][j];
} else {
//说明:
//因为我们的i 从1开始的, 因此公式需要调整成
//v[i][j]=Math.max(v[i-1][j], val[i-1]+v[i-1][j-w[i-1]]);
//v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
//为了记录商品存放到背包的情况,我们不能直接的使用上面的公式,需要使用if-else来体现公式
if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
//把当前的情况记录到path
path[i][j] = 1;
} else {
v[i][j] = v[i - 1][j];
}
}
}
}
//输出一下v 看看目前的情况
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + " ");
}
System.out.println();
}
System.out.println("============================");
//输出最后我们是放入的哪些商品
//遍历path, 这样输出会把所有的放入情况都得到, 其实我们只需要最后的放入
// for(int i = 0; i < path.length; i++) {
// for(int j=0; j < path[i].length; j++) {
// if(path[i][j] == 1) {
// System.out.printf("第%d个商品放入到背包\n", i);
// }
// }
// }
//动脑筋
int i = path.length - 1; //行的最大下标
int j = path[0].length - 1; //列的最大下标
while (i > 0 && j > 0) { //从path的最后开始找
if (path[i][j] == 1) {
System.out.printf("第%d个商品放入到背包\n", i);
j -= w[i - 1]; //w[i-1]
}
i--;
}
}
}
KMP算法-字符串匹配
public class KMPAlgorithm {
public static void main(String[] args) {
// TODO Auto-generated method stub
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
//String str2 = "BBC";
int[] next = kmpNext("ABCDABD"); //[0, 1, 2, 0]
System.out.println("next=" + Arrays.toString(next));
int index = kmpSearch(str1, str2, next);
System.out.println("index=" + index); // 15了
}
//写出我们的kmp搜索算法
/**
*
* @param str1 源字符串
* @param str2 子串
* @param next 部分匹配表, 是子串对应的部分匹配表
* @return 如果是-1就是没有匹配到,否则返回第一个匹配的位置
*/
public static int kmpSearch(String str1, String str2, int[] next) {
//遍历
for (int i = 0, j = 0; i < str1.length(); i++) {
//需要处理 str1.charAt(i) != str2.charAt(j), 去调整j的大小
//KMP算法核心点, 可以验证...
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j - 1];
}
if (str1.charAt(i) == str2.charAt(j)) {
j++;
}
if (j == str2.length()) {//找到了 // j = 3 i
return i - j + 1;
}
}
return -1;
}
//获取到一个字符串(子串) 的部分匹配值表
public static int[] kmpNext(String dest) {
//创建一个next 数组保存部分匹配值
int[] next = new int[dest.length()];
next[0] = 0; //如果字符串是长度为1 部分匹配值就是0
for (int i = 1, j = 0; i < dest.length(); i++) {
//当dest.charAt(i) != dest.charAt(j) ,我们需要从next[j-1]获取新的j
//直到我们发现 有 dest.charAt(i) == dest.charAt(j)成立才退出
//这时kmp算法的核心点
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j - 1];
}
//当dest.charAt(i) == dest.charAt(j) 满足时,部分匹配值就是+1
if (dest.charAt(i) == dest.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}
}
贪心算法
在每一步选择中都采取最好或最优(即最有利)选择。
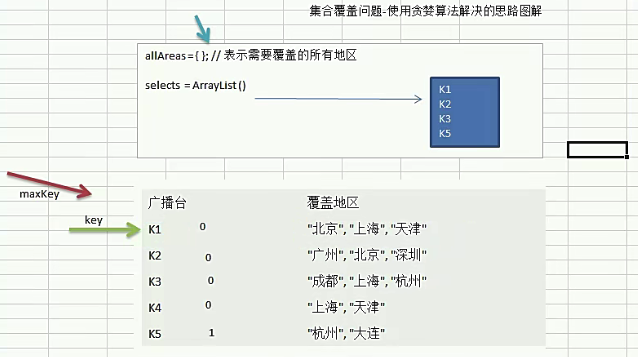
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
public class GreedyAlgorithm {
public static void main(String[] args) {
//创建广播电台,放入到Map
HashMap<String, HashSet<String>> broadcasts = new HashMap<String, HashSet<String>>();
//将各个电台放入到broadcasts
HashSet<String> hashSet1 = new HashSet<String>();
hashSet1.add("北京");
hashSet1.add("上海");
hashSet1.add("天津");
HashSet<String> hashSet2 = new HashSet<String>();
hashSet2.add("广州");
hashSet2.add("北京");
hashSet2.add("深圳");
HashSet<String> hashSet3 = new HashSet<String>();
hashSet3.add("成都");
hashSet3.add("上海");
hashSet3.add("杭州");
HashSet<String> hashSet4 = new HashSet<String>();
hashSet4.add("上海");
hashSet4.add("天津");
HashSet<String> hashSet5 = new HashSet<String>();
hashSet5.add("杭州");
hashSet5.add("大连");
//加入到map
broadcasts.put("K1", hashSet1);
broadcasts.put("K2", hashSet2);
broadcasts.put("K3", hashSet3);
broadcasts.put("K4", hashSet4);
broadcasts.put("K5", hashSet5);
//allAreas 存放所有的地区
HashSet<String> allAreas = new HashSet<String>();
allAreas.add("北京");
allAreas.add("上海");
allAreas.add("天津");
allAreas.add("广州");
allAreas.add("深圳");
allAreas.add("成都");
allAreas.add("杭州");
allAreas.add("大连");
//创建ArrayList, 存放选择的电台集合
ArrayList<String> selects = new ArrayList<String>();
//定义一个临时的集合, 在遍历的过程中,存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集
HashSet<String> tempSet = new HashSet<String>();
//定义给maxKey , 保存在一次遍历过程中,能够覆盖最大未覆盖的地区对应的电台的key
//如果maxKey 不为null , 则会加入到 selects
String maxKey = null;
while (allAreas.size() != 0) { // 如果allAreas 不为0, 则表示还没有覆盖到所有的地区
//每进行一次while,需要
maxKey = null;
//遍历 broadcasts, 取出对应key
for (String key : broadcasts.keySet()) {
//每进行一次for
tempSet.clear();
//当前这个key能够覆盖的地区
HashSet<String> areas = broadcasts.get(key);
tempSet.addAll(areas);
//求出tempSet 和 allAreas 集合的交集, 交集会赋给 tempSet
tempSet.retainAll(allAreas);
//如果当前这个集合包含的未覆盖地区的数量,比maxKey指向的集合地区还多
//就需要重置maxKey
// tempSet.size() >broadcasts.get(maxKey).size()) 体现出贪心算法的特点,每次都选择最优的
if (tempSet.size() > 0 &&
(maxKey == null || tempSet.size() > broadcasts.get(maxKey).size())) {
maxKey = key;
}
}
//maxKey != null, 就应该将maxKey 加入selects
if (maxKey != null) {
selects.add(maxKey);
//将maxKey指向的广播电台覆盖的地区,从 allAreas 去掉
allAreas.removeAll(broadcasts.get(maxKey));
}
}
System.out.println("得到的选择结果是" + selects);//[K1,K2,K3,K5]
}
}
普里姆算法(最小生成树)-修路问题
最小生成树(MST)

import java.util.Arrays;
public class PrimAlgorithm {
public static void main(String[] args) {
//测试看看图是否创建ok
char[] data = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int verxs = data.length;
//邻接矩阵的关系使用二维数组表示,10000这个大数,表示两个点不联通
int[][] weight = new int[][]{
{10000, 5, 7, 10000, 10000, 10000, 2},
{5, 10000, 10000, 9, 10000, 10000, 3},
{7, 10000, 10000, 10000, 8, 10000, 10000},
{10000, 9, 10000, 10000, 10000, 4, 10000},
{10000, 10000, 8, 10000, 10000, 5, 4},
{10000, 10000, 10000, 4, 5, 10000, 6},
{2, 3, 10000, 10000, 4, 6, 10000},};
//创建MGraph对象
MGraph graph = new MGraph(verxs);
//创建一个MinTree对象
MinTree minTree = new MinTree();
minTree.createGraph(graph, verxs, data, weight);
//输出
minTree.showGraph(graph);
//测试普利姆算法
minTree.prim(graph, 1);//
}
}
//创建最小生成树->村庄的图
class MinTree {
//创建图的邻接矩阵
/**
*
* @param graph 图对象
* @param verxs 图对应的顶点个数
* @param data 图的各个顶点的值
* @param weight 图的邻接矩阵
*/
public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
for (i = 0; i < verxs; i++) {//顶点
graph.data[i] = data[i];
for (j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
//显示图的邻接矩阵
public void showGraph(MGraph graph) {
for (int[] link : graph.weight) {
System.out.println(Arrays.toString(link));
}
}
//编写prim算法,得到最小生成树
/**
*
* @param graph 图
* @param v 表示从图的第几个顶点开始生成'A'->0 'B'->1...
*/
public void prim(MGraph graph, int v) {
//visited[] 标记结点(顶点)是否被访问过
int visited[] = new int[graph.verxs];
//visited[] 默认元素的值都是0, 表示没有访问过
// for(int i =0; i <graph.verxs; i++) {
// visited[i] = 0;
// }
//把当前这个结点标记为已访问
visited[v] = 1;
//h1 和 h2 记录两个顶点的下标
int h1 = -1;
int h2 = -1;
int minWeight = 10000; //将 minWeight 初始成一个大数,后面在遍历过程中,会被替换
for (int k = 1; k < graph.verxs; k++) {//因为有 graph.verxs顶点,普利姆算法结束后,有 graph.verxs-1边
//这个是确定每一次生成的子图 ,和哪个结点的距离最近
for (int i = 0; i < graph.verxs; i++) {// i结点表示被访问过的结点
for (int j = 0; j < graph.verxs; j++) {//j结点表示还没有访问过的结点
if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
//替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最小的边)
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
//找到一条边是最小
System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);
//将当前这个结点标记为已经访问
visited[h2] = 1;
//minWeight 重新设置为最大值 10000
minWeight = 10000;
}
}
}
class MGraph {
int verxs; //表示图的节点个数
char[] data;//存放结点数据
int[][] weight; //存放边,就是我们的邻接矩阵
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
克鲁斯卡尔算法(krushkal最小生成树)-公交站问题
最小生成树,用来求加权连通图
按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路
1、按权值排序从小到大
2、加入回路
import java.util.Arrays;
public class KruskalCase {
private int edgeNum; //边的个数
private char[] vertexs; //顶点数组
private int[][] matrix; //邻接矩阵
//使用 INF 表示两个顶点不能连通
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//克鲁斯卡尔算法的邻接矩阵
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ {0, 12, INF, INF, INF, 16, 14},
/*B*/ {12, 0, 10, INF, INF, 7, INF},
/*C*/ {INF, 10, 0, 3, 5, 6, INF},
/*D*/ {INF, INF, 3, 0, 4, INF, INF},
/*E*/ {INF, INF, 5, 4, 0, 2, 8},
/*F*/ {16, 7, 6, INF, 2, 0, 9},
/*G*/ {14, INF, INF, INF, 8, 9, 0}};
//大家可以在去测试其它的邻接矩阵,结果都可以得到最小生成树.
//创建KruskalCase 对象实例
KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
//输出构建的
kruskalCase.print();
kruskalCase.kruskal();
}
//构造器
public KruskalCase(char[] vertexs, int[][] matrix) {
//初始化顶点数和边的个数
int vlen = vertexs.length;
//初始化顶点, 复制拷贝的方式
this.vertexs = new char[vlen];
for (int i = 0; i < vertexs.length; i++) {
this.vertexs[i] = vertexs[i];
}
//初始化边, 使用的是复制拷贝的方式
this.matrix = new int[vlen][vlen];
for (int i = 0; i < vlen; i++) {
for (int j = 0; j < vlen; j++) {
this.matrix[i][j] = matrix[i][j];
}
}
//统计边的条数
for (int i = 0; i < vlen; i++) {
for (int j = i + 1; j < vlen; j++) {
if (this.matrix[i][j] != INF) {
edgeNum++;
}
}
}
}
public void kruskal() {
int index = 0; //表示最后结果数组的索引
int[] ends = new int[edgeNum]; //用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点
//创建结果数组, 保存最后的最小生成树
EData[] rets = new EData[edgeNum];
//获取图中 所有的边的集合 , 一共有12边
EData[] edges = getEdges();
System.out.println("图的边的集合=" + Arrays.toString(edges) + " 共" + edges.length); //12
//按照边的权值大小进行排序(从小到大)
sortEdges(edges);
//遍历edges 数组,将边添加到最小生成树中时,判断是准备加入的边否形成了回路,如果没有,就加入 rets, 否则不能加入
for (int i = 0; i < edgeNum; i++) {
//获取到第i条边的第一个顶点(起点)
int p1 = getPosition(edges[i].start); //p1=4
//获取到第i条边的第2个顶点
int p2 = getPosition(edges[i].end); //p2 = 5
//获取p1这个顶点在已有最小生成树中的终点
int m = getEnd(ends, p1); //m = 4
//获取p2这个顶点在已有最小生成树中的终点
int n = getEnd(ends, p2); // n = 5
//是否构成回路
if (m != n) { //没有构成回路
ends[m] = n; // 设置m 在"已有最小生成树"中的终点 <E,F> [0,0,0,0,5,0,0,0,0,0,0,0]
rets[index++] = edges[i]; //有一条边加入到rets数组
}
}
//<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
//统计并打印 "最小生成树", 输出 rets
System.out.println("最小生成树为");
for (int i = 0; i < index; i++) {
System.out.println(rets[i]);
}
}
//打印邻接矩阵
public void print() {
System.out.println("邻接矩阵为: \n");
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
System.out.printf("%12d", matrix[i][j]);
}
System.out.println();//换行
}
}
/**
* 功能:对边进行排序处理, 冒泡排序
* @param edges 边的集合
*/
private void sortEdges(EData[] edges) {
for (int i = 0; i < edges.length - 1; i++) {
for (int j = 0; j < edges.length - 1 - i; j++) {
if (edges[j].weight > edges[j + 1].weight) {//交换
EData tmp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = tmp;
}
}
}
}
/**
*
* @param ch 顶点的值,比如'A','B'
* @return 返回ch顶点对应的下标,如果找不到,返回-1
*/
private int getPosition(char ch) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == ch) {//找到
return i;
}
}
//找不到,返回-1
return -1;
}
/**
* 功能: 获取图中边,放到EData[] 数组中,后面我们需要遍历该数组
* 是通过matrix 邻接矩阵来获取
* EData[] 形式 [['A','B', 12], ['B','F',7], .....]
* @return
*/
private EData[] getEdges() {
int index = 0;
EData[] edges = new EData[edgeNum];
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
if (matrix[i][j] != INF) {
edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges;
}
/**
* 功能: 获取下标为i的顶点的终点(), 用于后面判断两个顶点的终点是否相同
* @param ends : 数组就是记录了各个顶点对应的终点是哪个,ends 数组是在遍历过程中,逐步形成
* @param i : 表示传入的顶点对应的下标
* @return 返回的就是 下标为i的这个顶点对应的终点的下标, 一会回头还有来理解
*/
private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
}
//创建一个类EData ,它的对象实例就表示一条边
class EData {
char start; //边的一个点
char end; //边的另外一个点
int weight; //边的权值
//构造器
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
//重写toString, 便于输出边信息
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">= " + weight + "]";
}
}
1.4.5.1.3. mst
1.4.5.1.3.1. 查找单链表中倒数第K个节点

1.4.5.1.3.2. 单链表反转


1.4.5.1.3.3. 从尾到头打印链表
可以利用栈,将各个节点压入栈,然后利用栈先进后出实现逆序打印(不改变链表结构)

1.4.5.1.3.4. 合并两个有序单链表,合并之后依然有序
1.4.5.1.3.5. 约瑟夫 josephu问题
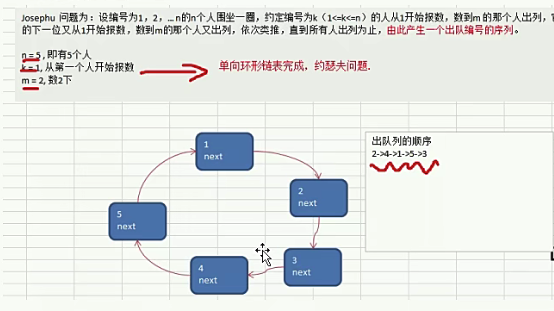
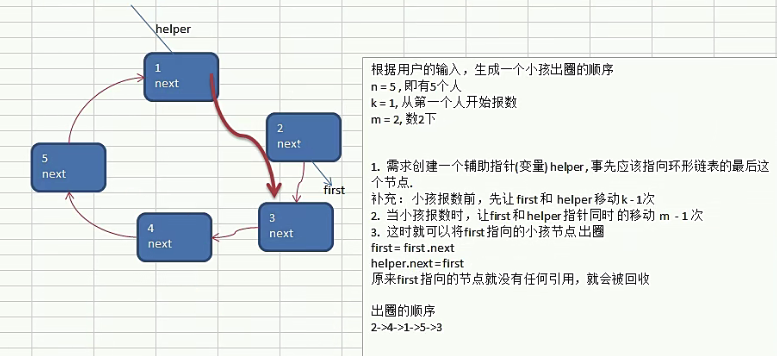
单向环形链表
枸建一个单向的环形链表思路
- 先创建第1个节点,让first指向该节点,并形成环彤
- 后面当我们每创建子个新的节点,就把该节点,加入到已有的环形谣表中即可
遍历环形链表 1.先让一个辅助指针(变量)curBoy,指向frst节点 2.然后通过一个while循环遍历该环形链表即可 aurBoy.next ==first结束
1.4.5.1.3.6. 递归-地图迷宫
//使用递归回溯来给小球找路 //说明 //1. map 表示地图 //2. i,j 表示从地图的哪个位置开始出发 (1,1) //3. 如果小球能到 map[6][5] 位置,则说明通路找到. //4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通 //5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
最短路径:定义不同策略,回溯比对各个策略的步数,找出最短
public class MiGong {
public static void main(String[] args) {
// 先创建一个二维数组,模拟迷宫
// 地图
int[][] map = new int[8][7];
// 使用1 表示墙
// 上下全部置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
// 左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//设置挡板, 1 表示
map[3][1] = 1;
map[3][2] = 1;
// map[1][2] = 1;
// map[2][2] = 1;
// 输出地图
System.out.println("地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//使用递归回溯给小球找路
//setWay(map, 1, 1);
setWay2(map, 1, 1);
//输出新的地图, 小球走过,并标识过的递归
System.out.println("小球走过,并标识过的 地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//使用递归回溯来给小球找路
//说明
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置,则说明通路找到.
//4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通
//5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
/**
*
* @param map 表示地图
* @param i 从哪个位置开始找
* @param j
* @return 如果找到通路,就返回true, 否则返回false
*/
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if (map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2; // 假定该点是可以走通.
if (setWay(map, i + 1, j)) {//向下走
return true;
} else if (setWay(map, i, j + 1)) { //向右走
return true;
} else if (setWay(map, i - 1, j)) { //向上
return true;
} else if (setWay(map, i, j - 1)) { // 向左走
return true;
} else {
//说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
//修改找路的策略,改成 上->右->下->左
public static boolean setWay2(int[][] map, int i, int j) {
if (map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if (map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 上->右->下->左
map[i][j] = 2; // 假定该点是可以走通.
if (setWay2(map, i - 1, j)) {//向上走
return true;
} else if (setWay2(map, i, j + 1)) { //向右走
return true;
} else if (setWay2(map, i + 1, j)) { //向下
return true;
} else if (setWay2(map, i, j - 1)) { // 向左走
return true;
} else {
//说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
}
1.4.5.1.3.7. 递归-八皇后
任意两个皇后不能处于同一行、同一列或者同一斜线,问有多少摆法。一个8*8回溯
一共有92解法一共判断冲突的次数15720次
注:可以用一个一维数组,arr[i] =val ; var表示i+1个皇后,放在第i+1行的第val+1 列
public class Queue8 {
//定义一个max表示共有多少个皇后
int max = 8;
//定义数组array, 保存皇后放置位置的结果,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
//测试一把 , 8皇后是否正确
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount); // 1.5w
}
//编写一个方法,放置第n个皇后
//特别注意: check 是 每一次递归时,进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯
private void check(int n) {
if (n == max) { //n = 8 , 其实8个皇后就既然放好
print();
return;
}
//依次放入皇后,并判断是否冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if (judge(n)) { // 不冲突
//接着放n+1个皇后,即开始递归
check(n + 1); //
}
//如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行得 后移的一个位置
}
}
//查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的皇后冲突
/**
*
* @param n 表示第n个皇后
* @return
*/
private boolean judge(int n) {
judgeCount++;
for (int i = 0; i < n; i++) {
// 说明
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
// n = 1 放置第 2列 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
//3. 判断是否在同一行, 没有必要,n 每次都在递增
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
//写一个方法,可以将皇后摆放的位置输出
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}